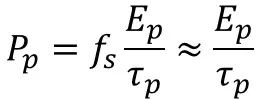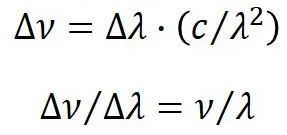The most straightforward method of generating laser pulses is to add a modulator to the outside of the continuous laser. This method produces pulses in the fastest picosecond range, which is simple but wastes light energy and the peak power does not exceed the continuous light power. Therefore, a more efficient method of generating laser pulses is intracavity modulation, where the energy is stored in the off-time of the pulse train and released in the on-time. A comparison of the two methods is as follows.
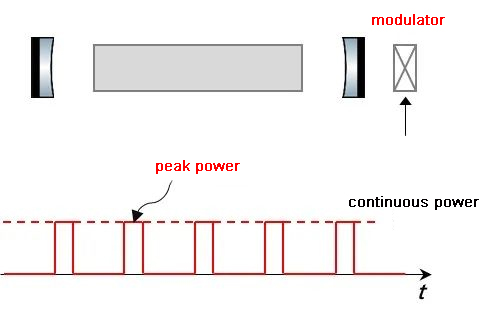
Extracavity modulation
Low peak power
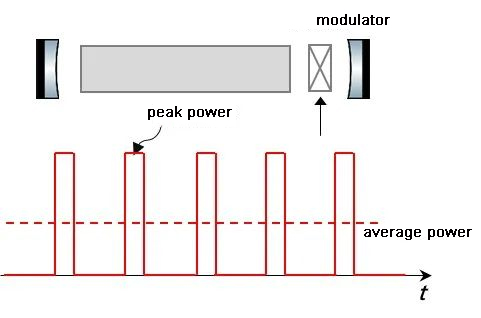
Intracavity modulation
High peak power
The four common techniques for generating pulses by modulation within the laser cavity are gain switching, Q-switching (loss switching), cavity inversion and mode-locking.
Gain switches produce short pulses by modulating the pump power. For example, semiconductor gain-switched lasers are capable of generating pulses of a few nanoseconds to a hundred picoseconds by current modulation. Although the pulse energy is low, this method is very flexible, offering, for example, adjustable re-frequencies and pulse widths. A femtosecond gain-switched semiconductor laser was reported by researchers at the University of Tokyo in 2018, signalling a breakthrough in a 40-year technology bottleneck.
·
Strong nanosecond pulses are typically generated by a Q-switched laser, where the laser is emitted in several round trips within the cavity with pulse energies in the range of a few millijoules to a few joules, depending on the size of the system.
Medium-energy (typically below 1 μJ) picosecond and femtosecond pulses are mainly generated by mode-locked lasers, where one or more ultrashort pulses are present in a continuous cycle within the laser resonant cavity, with the intracavity pulses emitted one at a time through the output coupling mirror, typically at heavy frequencies between 10 MHz and 100 GHz. An all normal dispersion (ANDi) dissipative soliton femtosecond fibre laser setup is shown below and can be built using mostly standard Thorlabs components (fibres, lenses, mounts and displacement tables).
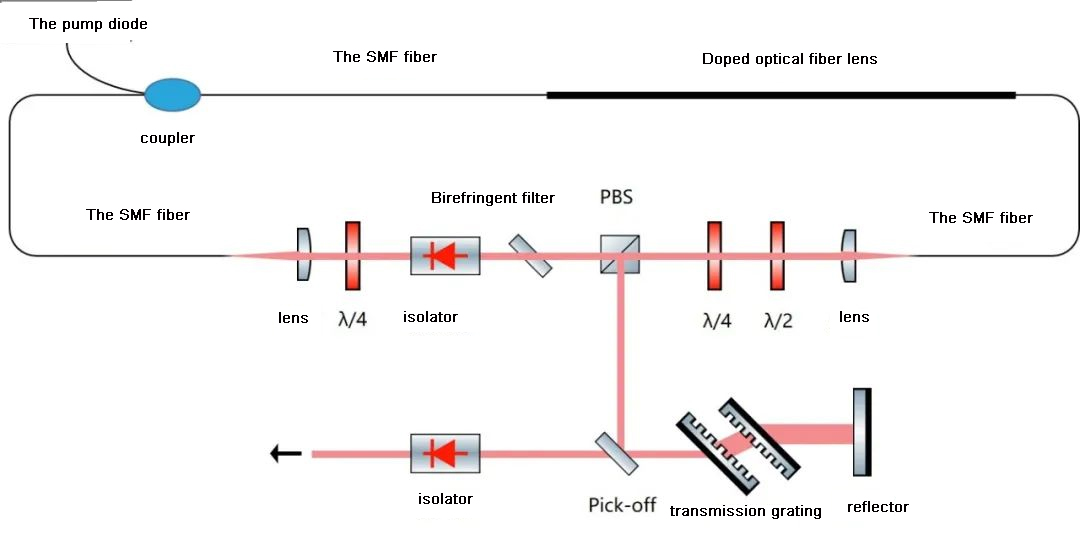
The cavity inversion technique can be used both for Q-switched lasers to obtain shorter pulses and for mode-locked lasers to increase the pulse energy at a lower re-frequency.
Dispersion compensation for 1.5 mm fused silica per reflection
Time and frequency domain pulses
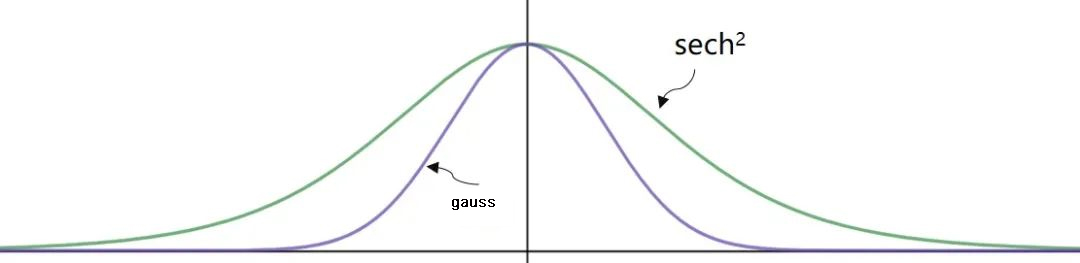
The linear shape of the pulse over time is generally relatively simple and can be expressed as a Gaussian and sech² function. The pulse duration (also known as pulse width) is most often expressed as a value of half-width-high (FWHM), i.e. the width across which the optical power is at least half the peak power; short pulses in the nanosecond range are generated by Q-switched lasers, and ultrashort pulses (USP) in the tens of picoseconds to femtoseconds range are generated by mode-locked lasers. High-speed electronics can only measure tens of picoseconds at the fastest, and shorter pulses can only be measured with the aid of purely optical techniques such as autocorrelators, FROG and SPIDER.
If the pulse shape is known, the relationship between pulse energy (Ep), peak power (Pp) and pulse width (p) is calculated according to the following equation.
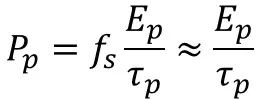
where fs is a coefficient related to the shape of the pulse and is approximately 0.94 for Gaussian pulses and 0.88 for sech² pulses, but is generally approximated by 1.
The bandwidth of a pulse can be expressed as frequency, wavelength or angular frequency. If the bandwidth is small, the wavelength and frequency bandwidths are converted using the following equation, where λ and ν are the central wavelength and frequency, respectively, and Δλ and Δν are the bandwidths expressed in terms of wavelength and frequency, respectively.
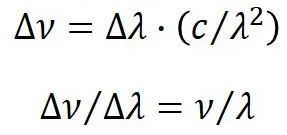
Bandwidth-limited pulses have thesmallest spectral width without chirp for a given pulse shape, when we call them bandwidth-limited or Fourier transform-limited pulses, and the product of the pulse time and frequency bandwidth is a constant called the time-bandwidth product (TBP). The time-bandwidth product of the bandwidth-limited Gaussian and sech² pulses is approximately 0.441 and 0.315 respectively; from this the actual pulse chirp and cumulative group delay dispersion can also be calculated.
1 ms (milliseconds) = 10−3 s | 1 ps (picosecond) = 10−12 s |
1 μs (microsecond) = 10−6 s | 1 fs (femtosecond) = 10−15 |
1 ns (nanosecond) = 10−9 s | 1 as (asec) = 10−18 s |
Pulse width influencing factors
While pulses of nanoseconds or longer propagate with little change in pulse width, even over long distances, ultrashort pulses may be affected by a variety of factors.
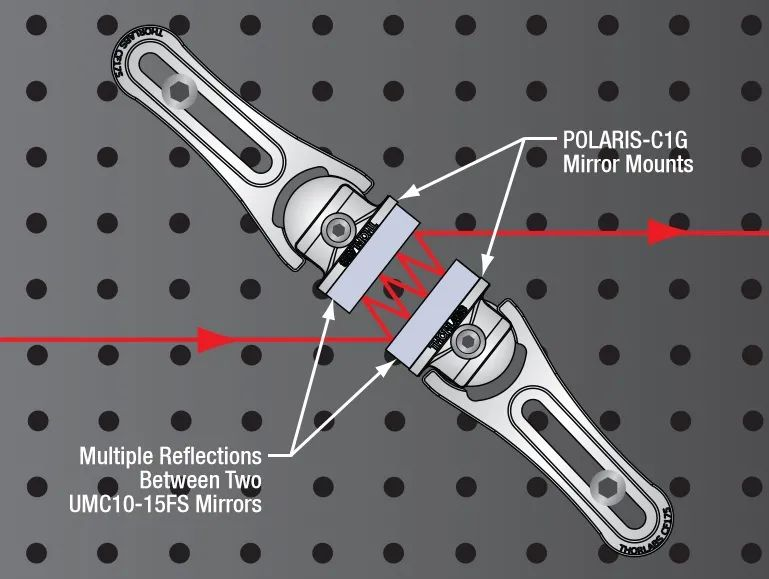
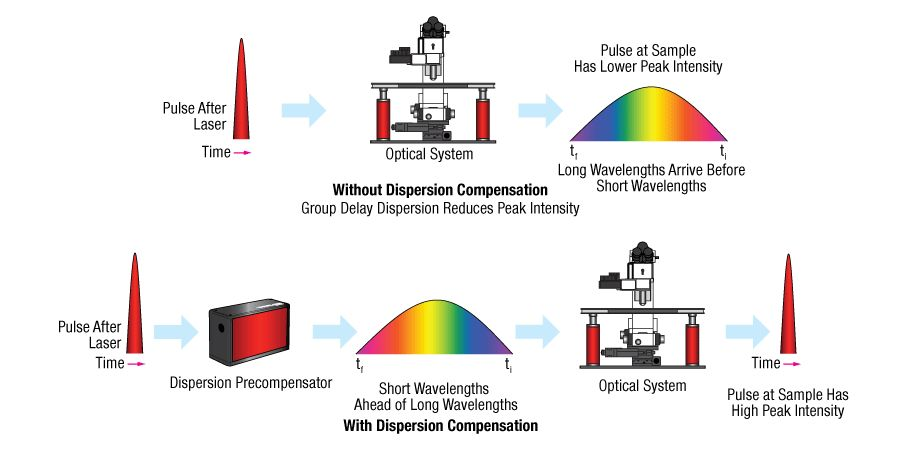
Chromatic dispersion can lead to large pulse spreads, but can be recompressed with the opposite dispersion, as shown in the diagram below, which shows how the Thorlabs femtosecond pulse compressor works to compensate for microscope dispersion.
The non-linearity does not generally affect the pulse width directly, but it does lead to a wider bandwidth, making the pulse more susceptible to dispersion as it propagates.
Any type of optical fibre (including other gain media with limited bandwidth) may affect the bandwidth or the shape of the ultrashort pulse, and a reduction in bandwidth may lead to time broadening; there are also cases where the pulse width of a strongly chirped pulse becomes shorter as the spectrum narrows.